Úloha podobného charakteru je známa v matematike pod názvom Buffonova ihla alebo Buffonova úloha. Jej teoretické riešenie však je oveľa náročnejšie než riešenie úlohy, ktorú budeme prezentovať. Uvažujeme štvorec so stranou 2, do ktorého je vpísaný kruh (s polomerom r = 1). Nech vrcholy tohto štvorca sú A[0;0], B[2;0], C[2;2], D[0;2]. Náhodne zvoľme n bodov vo štvorci a počítajme koľko z nich padne do kruhu. Označme tento počet m. Potom podiel
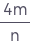
pre dostatočne veľké n určuje približne hodnotu čísla π.
Riešenie. Pravdepodobnosť, že náhodne zvolený bod vo štvorci so stranou 2 padne do kruhu, ktorý je do neho vpísaný sa podľa geometrickej pravdepodobnosti rovná podielu obsahu tohto kruhu a obsahu štvorca
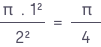
Ak by sme túto úlohu simulovali na počítači, tak budeme náhodne n-krát generovať dve nezávislé čísla x a y z intervalu (0,2) s rovnomerným rozdelením a testovať či padnú do kruhu so stredom v bode S[1;1] a polomerom 1, teda či spĺňajú podmienku

Počet tých prípadov, ktoré spĺňajú uvedenú podmienku označme m.
Ak n je dostatočné veľké, tak podiel m/n určuje približne hodnotu π/4. Potom podiel 4m/n určuje približne hodnotu Ludolfovho čísla π.
