PAMÄTÁTE SI NA TO, KEĎ NEJAKÍ DVAJA SPOLUŽIACI VO VAŠEJ ŠKOLSKEJ TRIEDE ALEBO KOLEGOVIA NA PRACOVISKU MALI NARODENINY V ROVNAKÝ DEŇ? HOVORILI STE SI, ŽE TO JE ZAUJÍMAVÉ A NEPRAVDEPODOBNÉ? NAPADLO VÁM ZISTIŤ, AKÁ JE VÔBEC PRAVDEPODOBNOSŤ TAKEJTO UDALOSTI? KOĽKO MYSLÍTE, ŽE POTREBUJETE NÁHODNE VYBRANÝCH ĽUDÍ V JEDNEJ MIESTNOSTI, ABY PRAVDEPODOBNOSŤ, ŽE V DANEJ SKUPINE BUDÚ MAŤ DVAJA ĽUDIA NARODENINY V ROVNAKÝ DEŇ, BOLA TAKMER 100%? MOŽNO VÁS VÝSLEDKY PREKVAPIA.
Kým začneme počítať, budú sa nám hodiť nasledujúce základné vlastnosti pravdepodobnosti. Jedna z nich je, že pokiaľ spočítam pravdepodobnosť opačného javu, než ktorý mám zadaný, potom pravdepodobnosť zadaného javu je dopočet do 1 („do sto percent“) – napríklad pravdepodobnosť, že na klasickej hracej kocke „padne 6“, je 1/6 , teda pravdepodobnosť opačného javu „nepadne 6“ je 1 – 1/6 = 5/6 . Druhou vlastnosťou pravdepodobnosti, ktorú využijeme, je samotný výpočet pravdepodobnosti. Ten sa dá zjednodušiť na výpočet pomocou podielu počtu „vyhovujúcich“ výsledkov nášho javu (označme ako k) a počtu všetkých možných výsledkov (označme ako m) – teda pravdepodobnosť je k/m. V našom príklade s kockou je k = 1, pretože vyhovujúci výsledok je len jeden (6 sa na kocke vyskytuje iba raz). A počet všetkých možných výsledkov m = 6, pretože na kocke sa vyskytuje 6 čísel. Posledná užitočná vlastnosť je, že pokiaľ počítame pravdepodobnosť „po častiach“ (teda rozdelíme náš skúmaný jav na viac podjavov*[1]), pravdepodobnosť skúmaného javu je súčinom pravdepodobností všetkých rozdelených javov. Tu nebudeme zabiehať do detailov, ako a kedy to funguje. Dostali by sme sa až k podmieneným pravdepodobnostiam a ich vlastnostiam, čo pre účely pochopenia narodeninového paradoxu nebude nutné.
Začnime s tým, že sa stretneme s tromi priateľmi na večeri, sme teda celkovo štyria. Aká je pravdepodobnosť, že aspoň niektorí dvaja z nás budú mať narodeniny v rovnaký deň?
Tu už začneme využívať jednotlivé vlastnosti, čím úlohu výrazne zjednodušíme. Podľa prvej vlastnosti môžeme najskôr spočítať pravdepodobnosť, že nikto z nás nemá narodeniny v rovnaký deň, a neskôr dopočtom do jednotky zistíme pravdepodobnosť, že aspoň dvaja z nás majú narodeniny v rovnaký deň. To, povedané trochu špecifickejšie, znamená, že si môžeme opačný jav rozdeliť na štyri podjavy:
- prvý člen našej skupiny (je jedno, ktorým začneme) sa narodil kedykoľvek
- druhý sa musel narodiť v ktorýkoľvek deň okrem dňa, kedy sa narodil prvý
- tretí sa musel narodiť ktorýkoľvek deň okrem narodeninových dní prvých dvoch členov
- a konečne štvrtý člen nesmie mať narodeniny ani v jednom z troch predchádzajúcich dní
Ak sa pokúsime tento špecifický popis teraz popísať matematicky, dostaneme pomocou druhej vlastnosti, že:
- prvý člen sa mohol narodiť v ktorýkoľvek z 365 dní v roku – teda pravdepodobnosť, že sa tak stane, je 365/365*[2] = 1 (to nám hovorí, že sa niekedy musel narodiť, čo asi nikoho neprekvapí)
- druhý sa mohol narodiť len v zostávajúcich 364 dňoch, teda pravdepodobnosť, že sa tak stane, je 364/365
- tretí sa potom nesmel narodiť v deň narodenín 1. alebo 2. člena, a zostáva teda na neho len 363 dní, v ktorých sa narodiť mohol – pravdepodobnosť 363/365
- posledný má pravdepodobnosť podľa rovnakej schémy 362/365
Teraz pomocou tretej vlastnosti „počítania po častiach“ vynásobíme tieto štyri spočítané pravdepodobnosti, čím zistíme pravdepodobnosť opačného javu „nikto z nás nemá narodeniny v rovnaký deň“:
365/365 * 364/365 * 363/365 * 362/365 ≅ 98,4 %
A konečne teda pravdepodobnosť nášho zadaného javu, že aspoň dvaja z nás majú narodeniny v rovnaký deň, je 1,6 % (100 % – 98,4 % – dopočet do sto percent). Asi nikoho neprekvapí, že vyšla takto malá pravdepodobnosť. Za domácu úlohu si môžete rovnakým spôsobom skúsiť spočítať pravdepodobnosť rovnakého javu v prípade, že by sa nás na večeru zišlo celkovo 6 ľudí (pre zvedavých výsledok je 4 %).
Poďme sa teraz pohrať s inou myšlienkou. Koľko náhodne vybraných ľudí potrebujeme umiestniť do jednej miestnosti, aby nami skúmaná pravdepodobnosť, že aspoň dvaja ľudia majú narodeniny v rovnaký deň, bola aspoň 50 %?
Koľko ľudí by ste hádali vy? 100? Alebo 200? Alebo myslíte, že 50 ľudí by už stačilo? Ako to spočítať viacmenej už vieme, využijeme úplne rovnaký postup ako v predošlom prípade. Označme si teraz len počet neznámych ľudí, ktorý hľadáme, ako n. Pre opačný jav „nikto nemá narodeniny v rovnaký deň“ dostaneme nasledujúci výpočet:
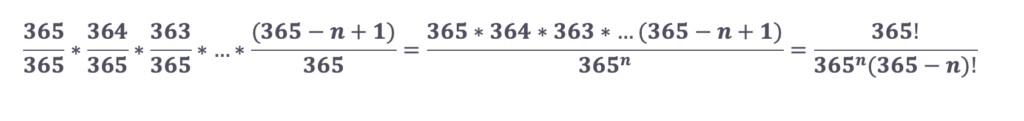
n = 1, 2, 3, …, 365 a ! znamená faktoriál čísla*[3]
Pokiaľ by sme za n dosadili teraz 4, dostaneme výsledok z minulého príkladu – môžeme si to jednoducho overiť:
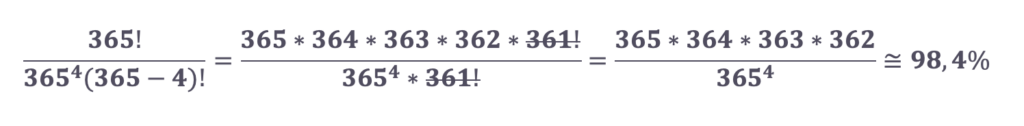
Nakoľko hľadáme odpoveď, kedy pravdepodobnosť pre jav „aspoň dvaja ľudia majú narodeniny v rovnaký deň“ je aspoň 50 %, opačný jav musí mať menšiu pravdepodobnosť než 50 %. A to je to, čo teraz budeme hľadať. Teda akú hodnotu dosadiť za n, aby vzťah vyššie dal hodnotu menšiu ako 50%, pričom budeme hľadať najmenšie také číslo, pri ktorom to platí. Nájsť totiž akékoľvek nie je ťažké, môžeme jednoducho vziať n = 366 -> týmto dostaneme pravdepodobnosť rovnajúcu sa presne 0 %. Čo je logické, pretože ak budeme mať 366 ľudí, tak aj keby 365 z nich malo narodeniny každý v jednom dni v roku, potom už ten 366. človek musí mať zákonite narodeniny ako jeden z tých 365 ľudí (pripomínam, že sa neberie do úvahy prestupný rok). Teda pravdepodobnosť, že nikto z 366 ľudí nemá narodeniny v rovnaký deň, je nulová. Poďme teda hľadať ono najmenšie n – skúsime dosadiť 100, ktoré sme hádali na začiatku. Tým dostaneme hodnotu 0,00003 %. Wow, to je veľmi malá pravdepodobnosť, že? Bude teda potrebné rozhodne hľadať nejaké číslo menšie – skúsme napríklad 50. Po dosadení dostaneme 2,96 %. Ako je to možné, že tak málo? Dobre, nebudem vás dlho napínať. Po chvíľke hádania a počítania by ste dospeli až k číslu 23, ktoré keď dosadíme do vzťahu, dostaneme pravdepodobnosť 49,27 %. Z toho vyplýva, že pravdepodobnosť hľadaného javu, že aspoň dvaja ľudia v skupine 23 ľudí majú narodeniny v rovnaký deň, sa rovná 50,73 %, čo bolo to, čo sme hľadali. Je možné, že v takto malej skupine 23 ľudí už je to päťdesiat na päťdesiat, že aspoň dvaja ľudia zdieľajú rovnaký deň narodenín? Áno je, a je to dané tým, že sa nesústredíme na jedného človeka v skupine, ktorého deň narodenia porovnávame s ostatnými, ale porovnávame narodeniny akýchkoľvek možných párov, ktoré týchto 23 ľudí tvorí.
Týchto párov je (23 * 22) / 2 = 253, čo je oveľa viac ako polovica dní v roku. V tomto kontexte už to tak nelogicky nevyzerá, že?
Na záver by som vypichol ešte jedno číslo, ktorým je číslo 69. Pokiaľ ho dosadíme do vzťahov vyššie, zistíme, že pravdepodobnosť, že medzi 69 náhodne vybranými ľuďmi sú aspoň dvaja, ktorí majú narodeniny v rovnaký deň, je 99,9 %. Dá sa povedať, že už je takmer isté, že medzi 69 ľuďmi sa nájdu dvaja, ktorí majú narodeniny v rovnaký deň.
Na týchto príkladoch je dobre ilustrované, že náš rozum sa dokáže pomerne ľahko pomýliť, pokiaľ necháme pracovať iba intuíciu. Stále si myslíte, že je to taká náhoda, keď sa stretnú dvaja ľudia v školskej triede, ktorí majú narodeniny v rovnaký deň?
*[1] Vybrané podjavy musia mať tú vlastnosť, že náš skúmaný jav je totožný s tým, že nastanú všetky podjavy súčasne.
*[2] V celom článku sme počítali s predpokladom, že sa ľudia rodia počas roka rovnomerne a nezávisle na sebe a že neexistuje prestupný rok. Je to síce mierne zjednodušenie, ktoré ale na myšlienke nič nepokazí.
*[3] Pre pripomenutie faktoriál čísla x sa počíta tak, že sa vynásobia všetky prirodzené čísla, ktoré sú menšie než dané x. Napr. 5! = 5 * 4 * 3 * 2 * 1 = 120. Faktoriál má jednu krásnu vlastnosť, že takto usporiadané súčinitele môžete kedykoľvek prestať vypisovať a za posledný z nich pripísať faktoriál bez toho, aby ste týmto postupom zmenili výsledok, napr. 5! = 5 * 4! = 5 * 4 * 3! = 5 * 4 * 3 * 2! = 5 * 4 * 3 * 2 * 1 = 120.
