Špecifický a senzitívny test alebo podmienená pravdepodobnosť v praxi

Ochorenie sa vyskytuje vzácne u 1 % ľudí. Prítomnosť ochorenia sa testuje citlivým vyšetrením, ktoré indikuje ochorenie (pozitívny výsledok) s pravdepodobnosťou 95 % u chorých a s pravdepodobnosťou 70 % zamieta ochorenie (negatívny výsledok) u zdravých ľudí, t.j. prevalencia ochorenia je 1 %, senzitivita testu je 95 % a špecificita testu je 70 %.

Ďalej sa u pozitívne vyšetrených vykonáva ešte druhé špecifické vyšetrenie. To u zdravého človeka vylúči ochorenie s pravdepodobnosťou 99 %, zatiaľ čo u chorého  človeka vylúči ochorenie s pravdepodobnosťou 10 %.

Aká je pravdepodobnosť, že je človek chorý, ak bol označený druhým testom za chorého, a aká je pravdepodobnosť, že je človek zdravý, ak bol druhým testom označený za zdravého?

Pravdepodobnosť výskytu ochorenia je P(N) = 0,01, senzitivita prvého testu je P(+1|N) = 0,95 a jeho špecificita P(-1|Z) = 0,7.

Pravdepodobnosť, že je človek chorý, ak bol označený prvým testom za chorého, je

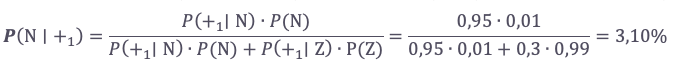
Pravdepodobnosť, že je človek zdravý, ak bol označený prvým testom za zdravého, je

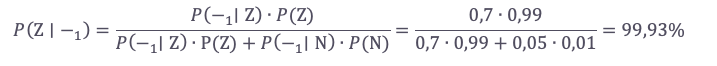
Pokiaľ je človek označený prvým testom za chorého, pravdepodobnosť, že je zdravý, P(Z|+1) = 1 – P (N|+1), je veľmi vysoká – 96,9 % (je to vďaka tomu, že ochorenie sa v populácii vyskytuje veľmi vzácne). Preto sa používa druhý špecifický test, ktorý je na prvom teste nezávislý a pre ktorý podľa zadania platí P(+2|N) = 0,90 a P(-2|Z) =0,99. Ďalej budeme používať značenie p, pokiaľ obidva testy dopadli pozitívne, teda p = +1 +2 , a n, pokiaľ prvý test dopadol negatívne alebo pokiaľ prvý test dopadol pozitívne a zároveň druhý negatívne, t.j. n = -1 u + 1-2.

Pravdepodobnosť pozitívneho nálezu u chorého človeka je teda

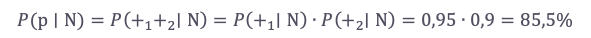
Pravdepodobnosť pozitívneho nálezu u zdravého človeka je

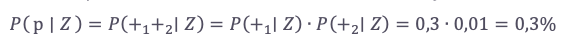
Pravdepodobnosť, že je človek chorý, pokiaľ má po oboch testoch pozitívny nález, je

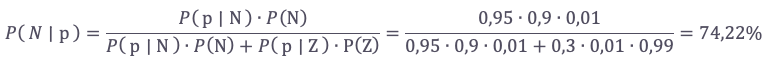
Pravdepodobnosť, že je človek zdravý, pokiaľ má negatívny nález je

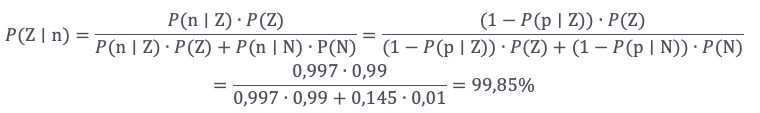
Fakt, že je pravdepodobnosť P(Z|n) menšia než pravdepodobnosť P(Z|-1), je daný tým, že jav n = -1 u +1-2 v sebe zahŕňa aj prípady, kedy prvý test dopadol pozitívne a kedy o výsledku druhého testu nič nevieme, keď prvý test dopadol negatívne. Pravdepodobnosť javu P(Z| -1 -2) je v súlade s očakávaním väčším než P(Z| -1).